Introduction
Our research explored the relations among coding theory, information theory, and related areas of computer science and mathematics. In error control coding, our team is concerned with the design, performance analysis and decoding of efficient modern error control systems such as wavelet codes, rateless codes, low density parity check codes (LDPC) and other types of iterative coding schemes. We are particularly interested in coding techniques for erasure channels, unequal error protecting codes, rate compatible codes, nonuniform codes, and two-dimensional codes for digital communication/storage systems and wireless ad hoc networks.
Rate-compatible coding
In designing an error correcting system for a time-invariant channel, we choose a code with a fixed rate and correction capability that adapts to the worst channel condition. However, in a mobile adaptive network the channel is time-varying, and different types of data require different error protection needs. Therefore, to maintain an acceptable quality of service, we need to change the coding rate during transmission. A natural solution to such a problem is the usage of a class of codes instead of a single code, depending on the quality of the channel. It is not practical to switch between multiple encoders and decoders, but we want to have one `good' code whose encoder and decoder are modified according to the rate without losing the good properties of the code. An interesting solution to this is the technique of puncturing. In this method, to change the rate of a code to a higher rate, we puncture (delete) a subset of the codeword bits. We study punctured LDPC codes over BEC and extend it to other MBIOS channels. We intend to derive bounds on the degradation of performance of punctured LDPC ensembles as a function of puncturing fraction. Using which, we plan to arrive at criteria for good puncturing patterns and degree distributions. We then intend to investigate the effect of puncturing on finite-length LDPC codes. We analyze this over BEC using a graph-theoretic approach and extend this analysis to random puncturing over other MBIOS channels. Finally, we plan to optimize the puncturing patterns to minimize the loss of performance due to puncturing in finite length cases.
LDPC Codes for Data Frames

In many applications, especially multimedia applications, not all parts of data have equal importance. Therefore, it is desirable to have a coding scheme that provides unequal error protection (UEP). We proposed two schemes to construct LDPC codes that are suitable for UEP. The first scheme is based on partially-regular LDPC codes. The proposed ensemble for the second scheme is a combination of two conventional bipartite graphs. We derived density evolution formulas for both the proposed UEP-LDPC ensembles. Using the density evolution formulas, high performance UEP codes were found. The proposed codes were also shown to have linear encoding complexity, which is very desirable for practical applications.
LDPC Decoding Algorithms
The performance of LDPC codes using the message passing algorithm over the binary erasure channel BEC has been extensively studied. Over BEC, it is well known that the iterative message passing algorithm stops if the set of erasures in the received codeword contains a stopping set although it may be the case that ML decoding may succeed in recovering the information bits completely. We note that even though the message passing algorithm is inferior to the ML decoding, it is practical and is a linear time algorithm. Interestingly, it can be noted that one can attribute to the set of parity check equations that a linear block code satisfies, an "abstract" vector space structure over the same field as that of the code. Therefore, if a received codeword is ML-decodable but not decodable by iterative message passing algorithm; thus, after the iterative decoder halts, there exists a set of parity check equations using which we can recover all the bits in the stopping set. Although we have not proved this yet, the structure of the stopping set is such that the knowledge of few unknown bits is enough to always complete the decoding if a received codeword is ML-decodable. Therefore, it may be possible to improve the performance if we can improve the standard message passing algorithm. This is particulary important for the short-length LDPC codes for which a good optimization methodology is lacking. We consider the improved decoding for both BEC and other memoryless binary input output symmetric channels (MBIOS). The intention is to analyze graph theoretic classification of stopping sets to evaluate the gain in performance with these algorithms. This characterization will eliminate the usage of simulations in the previously improved algorithms, making these viable for algorithmic implementation. We propose to prove that these algorithms are fast and have the same order of complexity as that of the standard message-passing
Wavelet Codes
In the past, the developments in wavelet decompositions and filter bank theory focused almost exclusively on real or complex fields. We develop the theory of finite-field wavelet transforms that provides a general wavelet decomposition of sequences defined over finite fields. This is an approach that has a rich history in signal processing for the representation of real-valued signals, but it has been lacking in the finite-field case. We introduce elementary paraunitary building blocks and a factorization technique that are specialized to obtain a complete realization for all paraunitary filter banks over fields of characteristic two. The work has led to a basis for a unified development of finite field wavelets and error control coding. We derived wavelet representations of many previously known codes. We find new codes such as self-dual codes and two-dimensional wavelet codes. We develop maximum distance wavelet codes that are the best possible codes in that they correct the maximum number of errors for a given amount of redundancy. We introduce new time-varying convolutional codes that can be decoded faster than conventional convolutional codes. random coding approach to jointly solve for packet authentication and availability.
Rateless Codes
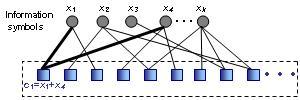
Rateless codes are a relatively new class of linear error-control codes. The idea behind the rateless codes is that every receiver continues collecting the encoded data until the decoding can be finished successfully. To generate an encoding symbol in a rateless code, a degree d is chosen randomly from a given degree distribution. Then, d information symbols are selected randomly and their values are XORed. This encoded symbol is then transmitted. Decoding of rateless codes is bases on belief propagation, which is an iterative algorithm. A receiver can recover k information symbols if it receives k encoding symbol, where . We investigated rateless codes for the following applications:
- UEP-Rateless Codes: We developed, for the first time, rateless codes that can provide UEP. We analyzed the proposed codes under both iterative decoding and maximum-likelihood decoding. Results are very promising and show the applicability of UEP-rateless codes in many important applications, such as transferring data frames or video/audio-on-demand streaming.
- Maximum-likelihood Decoding of Rateless Codes: we derived upper and lower bounds on maximum-likelihood (ML) decoding bit error probabilities of finite-length rateless codes over the binary erasure channel. The bounds on ML decoding are of interest, as it provides an ultimate indication on the system performance. Simulation results depict that the bounds are tight.
- Efficient Broadcast/Multicast Protocols via Rateless Coding: See our research section in SensorNets->Broadcast Protocols for details of these activities.