Quality Control in Approximate-Computing
The diminishing benefits from CMOS scaling has coincided with an overwhelming increase in the rate of data generation. Expert analyses show that in 2011, the amount of generated data surpassed 1.8 trillion GB and by 2020, consumers will generate 50 times this staggering figure. To overcome these challenges, both the semiconductor industry and the research community are exploring new avenues in computing. Two of the promising approaches are acceleration and approximation. Among accelerators, GPUs provide significant compute capabilities. Now GPUs process large amounts of real-world data that are collected from sensors, radar, environment, financial markets, and medical devices. As GPUs play a major role in accelerating many classes of applications, improving their performance and energy efficiency is imperative to enabling new capabilities and to coping with the ever-increasing rate of data generation. Many of the applications that benefit from GPUs are also amenable to imprecise computation. For these applications, some variation in output is acceptable and some degradation in the output quality is tolerable. This characteristic of many GPU applications provides a unique opportunity to devise approximation techniques that trade small losses in the quality of results for significant gains in performance and efficiency.
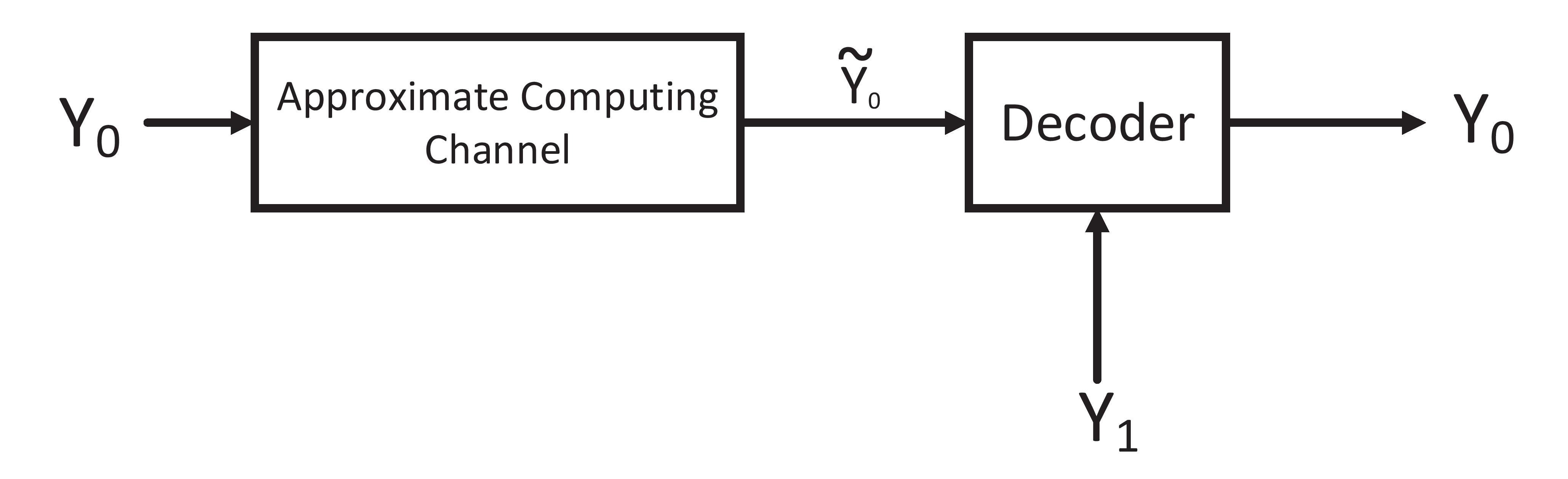
In this project, we extend Shannon’s mathematical foundation of communication to quality control in approximation. Approximation degrades the quality of the computed data and leads to imprecise outputs that should occasionally be corrected. This leads to several fundamental questions: Q1. Can we correct the errors made by approximate computing without losing its benefits? Q2. What is the mechanism that can operate within the minimum requirements and yet correct the errors? Inspired by Shannon’s work and the success of random codes in providing reliable communication over noisy channels, we propose to use coding techniques to correct the imprecise outputs from approximation. However, when employing approximation in GPUs, the precise outputs are not available for encoding in error correction. The research addresses this dilemma and related code design issues.