Learning via Inductive Logic Reasoning
Traditional machine learning techniques, which rely on learning the statistical dependency, often require large number of training data and they tend to overfit. They also generalize poorly for the unseen data if they are trained over small size training samples. Inductive Logic Programming (ILP), on the other hand, is a set of techniques to formulate and solve machine learning problems using (first order) logic algebra. Logic programming, as a subset of first-order logic, is mostly concerned with deductive inference. Instead, ILP is concerned with inductive inferences. In ILP, background knowledge, positive and negative training examples and the hypothesis can be uniformly expressed using the relational predicate logic. ILP techniques do not require large training examples and can generalize well. However, current ILP solvers suffer from their limited ability to learn recursion and to create new predicates as needed. In 2018, our team was able to develop neural networks that can learn Boolean relations among input variables. What distinguish these neural logic networks is its ability to represent the learned knowledge in an explicit form that is human readable. Later in 2018, using these Boolean networks, we could transform any ILP task into a differentiable problem and solve it using gradient optimizers. Our resulting ILP solver has desirable features such as recursion and predicate invention and thus can tackle several learning tasks that were previously unsuccessful with ILP techniques. The hypothesis or policy rules learned by the resulting ILP framework is human interpretable, and hence can be read, and verified by the expert observer. Moreover, since the language for the representation is chosen by the expert, it is possible to incorporate inductive biases into learning which can be a significant improvement in complex problems. Finally, it allows for the inclusion of human preferences and higher-level concepts and prior knowledge as the background knowledge into policy learning. As such our ILP is uniquely positioned for policy learning in network traffic monitoring or explainable AI in trust.
Inspired by all the above desirable characteristics of ILP, our current research objectives are to develop a new research paradigm at the intersection of differentiable ILP in graph reasoning tasks, temporal inductive reasoning, time of events prediction, defending adversarial attacks on machine learning, neuro-symbolic reinforcement learning, causality and rule based inference in network security, explainable AI for trust, classification task for large dataset, and decoding error correcting codes.
Differentiable ILP
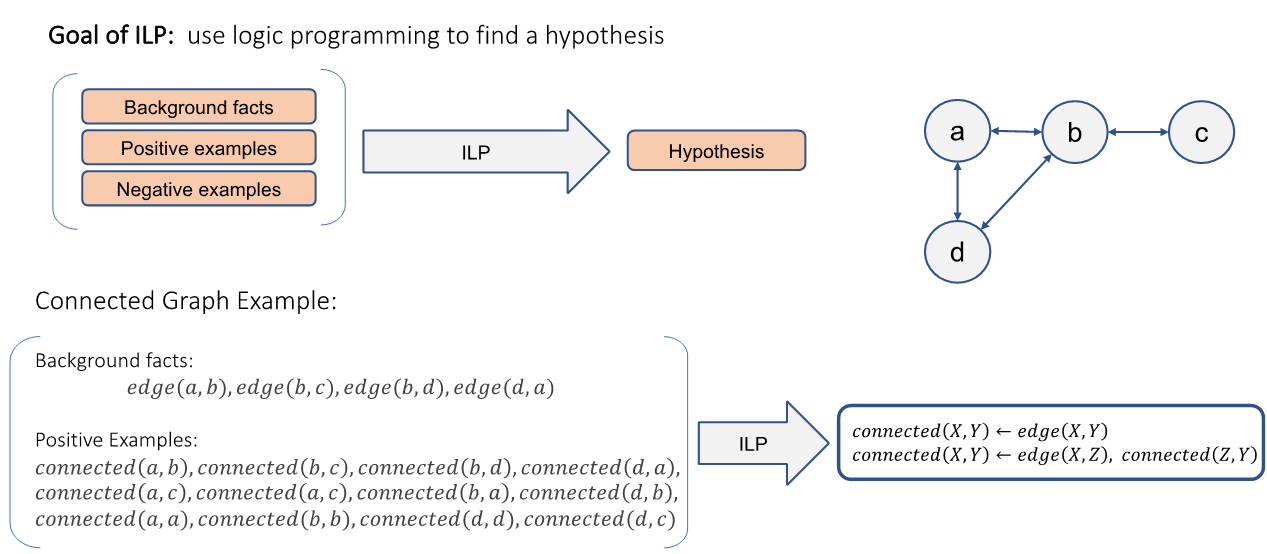
Inductive Logic Programming (ILP) is to learn a first-order logical formula based on background knowledge, positive examples and negative examples. To develop differentiable Inductive Logic Programming (ILP), we take two approaches: 1. Forward reasoning methods based on Neural-Logic Networks, 2. Backward reasoning method based on Random Walk on graphs.
Differentiable ILP via Neural-Logic Networks: The ability to learn Boolean logic in an explicit and interpretable manner is at the heart of our framework. Our team designed a differentiable neural networks dedicated to learn and represent Boolean functions in an explicit and efficient way. The general idea of representing and learning Boolean functions using neural networks is not new. There is significant body of research from the early days of machine learning using neural networks that is focused on the theoretical aspects of this problem. Some special Boolean functions such as parity-N and XOR has been the subject of special interest, as benchmark tasks for theoretical analysis. In principle, as was suggested by many works, any Boolean function can be learned by a multi-layer neural network equipped with proper activation functions. However, this approach is not always applicable. As an alternative to typical additive neurons, we propose a set of differentiable and multiplicative neurons which are designed with the specific function of learning Boolean functions efficiently and in an explicit manner which can be read and verified by human. We refer to these networks as differentiable Neural Logic (dNL) networks. We have demonstrated that the explicit representational power of the proposed dNL networks allows us to transform the inductive logic programming into a differentiable problem and solve it using gradient optimizers more efficiently than the existing neural ILP solvers.
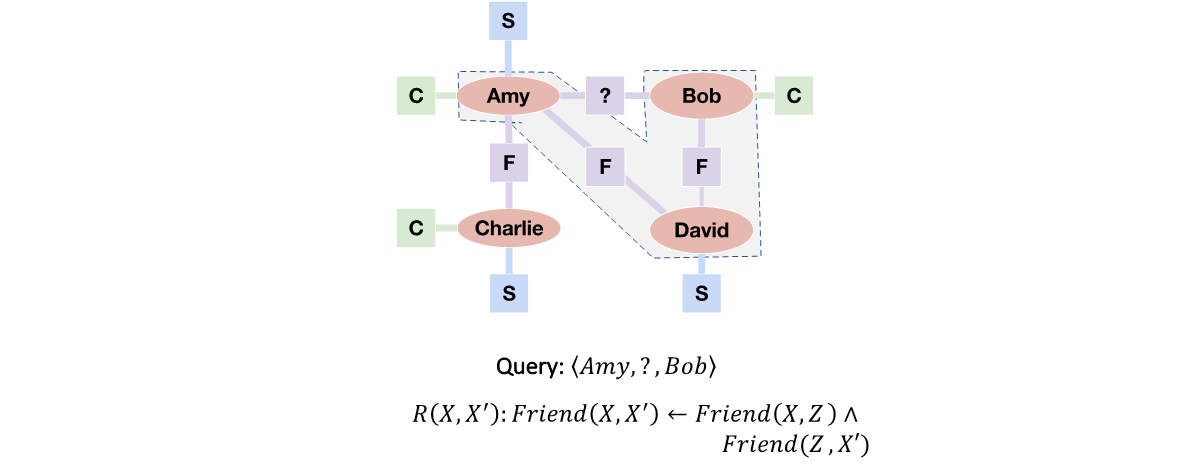
Differentiable ILP via Backward Reasoning over Graphs: Given a query, the differentiable ILP approach is to use the attention mechanism to softly select the predicate of each atom in the rule body. For ILP over knowledge graphs, in our early works, we assume the formula to be “chain-like” rules, i.e., the variables in the rule body form a path from the subject entity to the object entity of the query. We adopt the random walk strategy to find the path that is inductively supported. By introducing state vectors and matrix operators for different predicates, we convert the backward logical reasoning process over knowledge graphs into a set of matrix operations. For each step of random walk, we multiply the state vector by a weighted sum of all candidate predicate matrices. During the training, given a set of positive examples, we maximize the probability of arriving at the object entity from the subject entity via a walk on the graph. By using the Gradient Descent algorithm, we learn the best attention vectors which decide the weights of different predicates for each step in the walk.
Logical Reasoning over Graphs via ILP
Graph structures are widely present in many real-world datasets and form the foundations of a wide range of AI systems. For example, knowledge graphs (KGs) represent knowledge as a graph with nodes as the entities and the edges that connect them as the facts; temporal graphs represent the stream data such as video clips similarly as the KGs but also include the temporal information of the facts; and abstract syntax trees are widely used to represent the structural information of a piece of source code, which typically involves higher-order information.
Graph reasoning is one of the fundamental tasks for graph data and plays a critical role in many real-world applications such as question answering, drug discovery, recommender system, and program synthesis. The task involves inferring missing facts from the existing data. Such inference can be realized as a one-hop prediction task, where the reasoning model predicates the missing facts directly. Methods of this category include graph embedding methods, and GNN-based methods. While they excel in performance, they are not data efficient in training and lack explainability. Alternatively, missing facts can also be inferred by performing multi-hop “logical’ reasoning over the graph structure. This approach seeks to find an explicit local subgraph (e.g., a path or a tree) that logically supports the inference. Such reasoning on the graph has been studied extensively under the inductive logic programming (ILP) formalism; a variety of ILP methods are proposed to solve the task by generalizing the first order logic rule from the local subgraphs. Compared to the one-hop reasoning model, ILP methods lead to highly interpretable results and require far less data to train. However, existing ILP methods are limited where
- 1. The rules are restricted to chain-like Horn rules which are limited in terms of the expressive power.
- 2. They scale poorly with large graphs.
In this project we investigate the above problems.
Data Programming and Link/Entity Prediction via ILP (LOGICDP)
In this project, we investigate two inter related problems, namely, Data Programming and Link/Entity Prediction in Knowledge Graphs (KGs). Graph datasets are usually incomplete and new facts can be inferred from the existing facts. A large body of research has been proposed to address this task. For KG reasoning, a variety of graph embedding methods are proposed. These graph reasoning methods rely on standard supervised training, where the model is fed with a fixed set of data that are curated beforehand. Such training leads to a state-of-the-art performance when a large amount of data is available. On the other hand, the recent advances in data-centric AI and data programming aims at a new paradigm for training and evaluating ML models with weak supervision. Existing frameworks such as Snorkel show great potential in this direction but are also limited in applications where expert labeling functions are difficult or expensive to construct, and they do not utilize the rich semantic information in graphs to automate the process. In this work, we approach this problem by adopting the data programming (DP) paradigm, which aims at creating a large high-quality labeled dataset from a set of labeling functions that generate noisy, incomplete, and conflicting labels. We propose LOGICDP, a DP framework that creates training data for graph reasoning models. Compared to the existing domain-general DP frameworks, LOGICDP utilizes the ILP technique and can automatically generate labeling functions in the form of first-order logic rules from a small labeled set; LOGICDP also employs a budget-aware framework that refines the functions through weak supervision from an oracle.
ILP for Adversarial Defense in ML (LOGICDEF)
In this work, we use ILP to protect AI models against adversarial attacks. Deep learning models have achieved great success in many visual tasks, such as object classification and detection. However, these models are not robust in situations where an attacker can modulate the input with only small perturbations, since such data modulation can deceive the predictive ML models, e.g., cause them to misclassify objects in an object classification task. Many mechanisms have been proposed to defend against perturbation attacks. Some rely on empirical techniques, such as training with adversarial examples. Other methods such as certifiable defenses seek to protect the classifier by verifying its prediction is within a prescribed ball around the input. However, these methods are developed specifically for those specific attacks, and the computational expense and the architectural limitations they impose limit their practical applications. Despite their sophistication, we note that most of these attacks can be easily detected by humans. In contrast to machine learning models, humans recognize and describe objects using a component hierarchy and by correlating co-occurring ancillary scene features, properties, and entities. Inspired by this human capability, we argue that an effective defense should produce an explanation as to why the system is attacked, and by using a representation that is easily readable by a human user, e.g. a first order logic formalism in ILP. Given a potentially corrupted image, LOGICDEF generates the scene graph and examines the consistency among the graph elements with logic rules produced by ILP, and also applies common sense reasoning. In the long term, this research aims at providing an alternative way to inspect the behavior of ML models in most supervised tasks.
Temporal ILP Framework (TILP)
Modern machine learning models have provided new capabilities across a spectrum of applications in vision, reasoning, and natural language processing. However, these models are criticized for not incorporating temporal aspects explicitly into their models. Addressing this issue remains at the center of developing ML systems for real-world applications. In this project, we aim at developing a Temporal ILP (TILP) framework that would explicitly incorporate the time (or the interval of time) of events into the first order logic rule. In particular, we use random walk on temporal Knowledge Graphs (tKGs) to arrive at TILP. Unlike static KGs, the tKGs can capture the evolution and change of information over time, and hence, they are more realistic and general. Embedding methods are conventionally used to perform reasoning in tKGs. However, they require massive data, and they are not interpretable. However, due to the complexity that the notion of time introduces to the learning of the rules in ILP, an accurate graph reasoning, e.g., predicting new links between entities, is a challenging problem. To this end, we develop a differentiable framework for temporal logical rules learning, which leverages a constrained random walk mechanism and the introduction of simplified temporal operators. We compare our method with state-of-the-art methods on benchmark datasets. We show that our proposed framework can improve upon the performance of baseline methods while providing interpretable results. In particular, we consider various scenarios in which training samples are limited, data is biased, and the time range between training and inference are different. In all these cases, our method is superior to existing state-of-the-art methods.
Reasoning over Higher Order Graphs via ILP
Modern machine learning models have provided new capabilities across a spectrum of applications in vision, reasoning, and natural language processing. However, these models are criticized for being non-interpretable, data-inefficient, and vulnerable to subtle perturbations such as adversarial attacks and distribution shifts. Our research focuses on providing a principled solution to these issues through logic reasoning formalism: (1) we study the fundamental technique of inductive logic programming (ILP) that learns and represents patterns in knowledge graphs as first-order logic rules, providing an interpretable approach to various reasoning tasks on structured data, (2) Traditional ILP methods operate on traditional knowledge graph where no temporal information nor the higher-order relations are included. However, many real-world applications (e.g., such as video streams and abstract syntax trees) constantly involve such information. To this end, we propose to extend ILP methods to both the temporal domains and the hypergraphs where relations involve more than two entities, so that one can generalize FOL rules on complex data structures. In particular, we propose a random walk (RW) algorithm on a hypergraph, as RW is the fundamental mechanism of a family of widely used ILP methods, that is the backward-chaining methods.