Introduction
There has been a rapidly growing interest in studying biomarkers. Biomarkers are shown to have applications in the disease detection (e.g., cancer, heart disease, infection, epilepsy, Alzheimer, aging, etc). A biomarker may also be used to monitor how well the body responds to a treatment for a disease or condition. By definition, a biomarker is a characteristic that is objectively measured and evaluated as an indicator of normal biological processes, pathogenic (i.e., causing disease) processes or pharmacological responses to a therapeutic intervention.
Synthetic biology harnesses genetic engineering and computational solutions to redesign useful biological products. Living cells with genetically-encoded sensors engage in sensing, processing, and actuation based on environmental stimuli. Inspired by one of the long-term goals of synthetic biology to reliably engineer biological systems that perform human-defined functions such as sensing and monitoring, we propose to investigate several problems including identification of the biomarkers for each target disease, studying fundamental limits and develop algorithms for biomarker sensing via a group of engineered cells (i.e., a biosensor array). We study the biomarker sensing problem with potential applications in disease detection. We establish the rate-distortion theory for biomarker sensing and investigate as to how distortion can be minimized via an optimal quantizer. We also study sensor cell arrays in which sensing redundancy is achieved by using multiple sensors to measure several biomarker inputs simultaneously. We develop algorithms to solve the disease detection problem using the biomarkers measurements.
MicroRNA (miRNA) Sensing
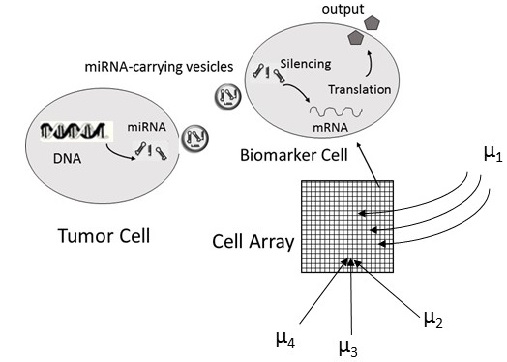
MicroRNAs are small non-coding RNA molecules that play a key role in inter-cell communication in humans. Irregular patterns over specific miRNAs are already linked to certain types of cancer and cardiac diseases. Hence, miRNA can serve as useful biomarkers of physiological state (disease), and some studies suggest circulating miRNAs may be used as a tool for therapeutic treatments as well. Synthetic biologists have already engineered biosensors with messenger RNA (i.e., mRNA) circuits that respond to miRNAs. The MicroRNAs influence cell gene expression by silencing the protein translation of mRNAs inside the cell. Prof. Fekri’s research proposes a small array of mRNA sensors that measures the concentration of hundreds of miRNAs which can then be used in a signal processing and machine learning algorithms to detect the target diseases. In particular, the research plans to develop a framework to identify the proper biomarkers for each disease, study the sensing problem, and develop the detection algorithms.
Density Evolution for Biomarker Sensing System Design

The research is focused on developing a novel general framework based on density evolution on graphs to optimize a compressive sensing/measurement system for the high-dimensional signal recovery. More specifically, assuming the signal x lies within a low-dimensional subspace, we want to give a general framework to design a sparse compressive linear sensing system ‘A’ that would allow recovery of high dimensional signal X from the low dimensional measurement. Additionally, we wish to provide preferential treatment for a sub-block of the signal x, i.e., a sub block with higher or more sensitive information would recover with better accuracy than the other components of the signal X.
At the core of our work is the application of density evolution in the message passing algorithm, which is previously used in designing the Low Density Parity Check Codes, LDPC, for the communication channels. Viewing the signal recovery as an inference problem, we transformed the problem of designing the sensing matrix (the linear measurement system) to the problem of graph connectivity. Then we investigated the impact of the graph connectivity on the behavior of the probabilistic message flows during decoding of the signal, from which we can obtain the constraints for designing the sensing matrix by forcing successful decoding.
We considered the setting where some components of x have unequal importance from the recovery perspective and we wish to design the sensing system to take into the account this desirable property in the recovery of the original X from the low dimensional samples. For example, recovery of the biomarker miRNAs (of say skin cancer) has higher importance than recovering non-biomarker miRNAs in the disease detection. This preferential sensing framework could also have many other practical applications such as image compression, i.e., JPEG compression, where coefficients corresponding to the low-frequency should be better preserved than the high- frequency part. Our objective in this part was consisted of three problems: (i) How do we obtain the corresponding density evolution equations for preferential reconstruction; (ii) How do we provide preferential treatment for sub-blocks of signal x with high-priority; and (iii) How do we formulate the design criteria as an optimization problem that can be efficiently solved.
Different from the regular reconstruction, we need two groups of density evolution equations, which separately track the means and variances of the message flows (in belief propagation over graph) between the high-priority variable nodes and check nodes and that between the low-priority variable nodes and check nodes of the graph. By placing more stringent constraints on the decoding error corresponding to the high-priority signal components, we come up with an optimization problem to design a sensing matrix which provides more accurate recovery of the high-priority entries of X.